

Surface area of pentagonal prism = 5ab + 5bh Surface area of trapezoidal prism = h (b + d) + l (a + b + c + d) Surface area of rectangular prism = 2(lb + bh + lh) Surface area of square prism = 2a 2 + 4ah Surface area of triangular prism = bh + (s1 + s2 + b)H Surface Area of Prisms = (2 × Base Area) + (Base perimeter × height) See the table below to understand this concept behind the surface area of various prisms: Shape The bases of different types of prisms are different so are the formulas to determine the surface area of the prism. There are seven types of prisms we read above based on the shape of the bases. The total surface area of a prism = Lateral surface area of prism + area of the two bases = (2 × Base Area) + Lateral surface area or (2 × Base Area) + (Base perimeter × height). The lateral surface area of prism = base perimeter × height The lateral area of a prism is the sum of the areas of all its lateral faces whereas the total surface area of a prism is the sum of its lateral area and area of its bases. There are two types of areas we read about, first, the lateral surface area of the prism, and second, the total surface area of the prism. Let us learn these two in the case of prisms. The two formulas are the area of the shape and volume of the shape. There are two basic formulas we read in geometry about all the respective 3-dimensional shapes. Trapezoidal Prism: A prism whose bases are trapezoid in shape is considered a trapezoidal prism.Octagonal Prism: A prism whose bases are octagon in shape is considered an octagonal prism.Hexagonal Prisms: A prism whose bases are hexagon in shape is considered a hexagonal prism.Pentagonal Prism: A prism whose bases are pentagon in shape is considered a pentagonal prism.Rectangular prism: A prism whose bases are rectangle in shape is considered a rectangular prism (a rectangular prism is cuboidal in shape).Square Prism: A prism whose bases are square in shape is considered a square prism.Triangular Prism: A prism whose bases are triangle in shape is considered a triangular prism.Oblique Prism: An oblique prism appears to be tilted and the two flat ends are not aligned and the side faces are parallelograms.Ī prism is named on the basis of the shape obtained by the cross-section of the prism.Right Prism: A right prism has two flat ends that are perfectly aligned with all the side faces in the shape of rectangles.There are two different prisms based on the alignment of the bases named: Prisms Based on the Alignment of the Identical Bases. Irregular Prism: If the base of the prism is in the shape of an irregular polygon, the prism is an irregular prism.Regular Prism: If the base of the prism is in the shape of a regular polygon, the prism is a regular prism.There are two types of prisms in this category named as: Prisms can be classified on the following basis: Prisms Based on the Type of Polygon, of the BaseĪ prism is classified on the basis of the type of polygon base it has.

Today, the surface area of a triangular prism remains a fundamental principle in geometry and continues to serve as a crucial element in a multitude of practical applications.Before reading about various types of prisms let us understand on what basis types of prisms can be obtained. Their studies on triangles, parallelograms, and three-dimensional shapes have greatly influenced contemporary understanding of geometry and the surface area of various shapes, including triangular prisms. While there is no definitive historical account of the origin of the triangular prism or its surface area concept, it can be traced back to ancient Greece, where mathematicians like Euclid and Pythagoras laid the groundwork for modern geometry. Moreover, artists and designers frequently employ triangular prisms in their creations, making the knowledge of surface area invaluable for conceptualizing and executing their work. In packaging design, calculating the surface area of a triangular prism helps optimize material usage, reduce waste, and minimize costs. For instance, in construction and architecture, the surface area plays a role in determining the stability and strength of structures, as well as insulation and energy efficiency. Triangular prisms, like other three-dimensional shapes, have numerous real-life applications that make understanding their surface area essential. The concept of surface area has broad applications in various fields, including engineering, architecture, and design, where it is crucial to estimate material requirements, costs, and structural integrity.
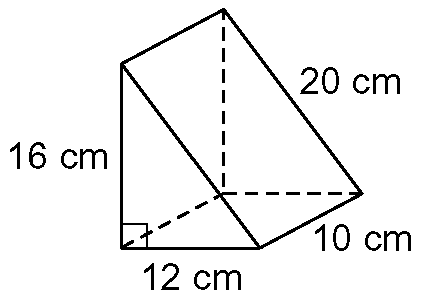
A triangular prism consists of two congruent triangles at the ends, known as bases, connected by three parallelogram-shaped lateral faces. The surface area of a triangular prism is a key concept in geometry that pertains to the total area covering the external faces of the three-dimensional shape.


 0 kommentar(er)
0 kommentar(er)
